Có một con Robot trên một ma trận ~n*m~. Robot này đang đứng ở vị trí ~(1, 1)~. Bạn có thể điều khiển con Robot này qua bên phải hoặc xuống dưới (nói cách khác nếu Robot đang ở ô ~(i, j)~ thì Robot có thể đi đến ô ~(i+1, j)~ hoặc ~(i, j+1)~) miễn sao Robot không đi ra ngoài ma trận. Nhiệm vụ của bạn là hãy đếm số cách đi của Robot sao cho Robot đi từ ô (1, 1) đến ô (n, m).

Input

Gồm ~1~ dòng chứa số nguyên ~n~ ~m~ ~(1 \le n \le 10^2)~.

Output

Ghi ra số cách đi khác nhau của Robot đi từ ô ~(1, 1)~ đến ô ~(n, m)~.

Sample Input 1

2 2

Sample Output 1

2

Sample Input 2

20 23

Sample Output 2

244662670200

• Sau khi đã trở thành master coder, Pitomon quyết định sẽ phát triển bản thân bằng cách lật đổ công ty google và tạo ra một đế chế mới của riêng mình. Để thực hiện kế hoạch táo bạo đó, Pitomon đã quyết định thực hiện bước đầu bằng cách tạo ra một công cụ tìm kiếm mới cạnh tranh với google.
• Pitomon tìm kiếm kho tàng dữ liệu của mình và thấy vài triệu tên người dùng mà anh mấy mua trên deepweb và anh ấy sẽ sử dụng dữ liệu đó để test công cụ mới của mình. Dữ liệu sẽ gồm ~n~ tên người dùng, mỗi tên người dùng không có dấu cách và chữ cái in hoa (chỉ gồm các kí tự từ ~a \rightarrow z~). Và yêu cầu đặt ra với bước đầu tiên của Pitomon, anh ấy sẽ kiểm tra thuật toán của mình ~m~ lần, mỗi lần sẽ có ~1~ sâu kí tự ~S~ là tên người dùng mà anh ấy nhập vào, và máy tính phải in ra liệu tên đó có nằm trong bộ dữ liệu của mình hay không, nếu có thì in ra ~1~ và nếu không thì in ra ~0~.
• Vì máy tính của anh ấy đã bị hư nên các bạn hãy giúp anh ấy thực hiện giấc mơ ấy nhé!!

Input

• Dòng đầu tiên chứa 2 số nguyên ~n, m~ (~1 \leq n, m \leq 10^5~) là số lượng dữ liệu đầu vào và số lần thử của Pitomon.
• ~n~ dòng tiếp theo, mỗi dòng gồm một chuỗi kí tự (độ dài không vượt quá ~20~ và chỉ gồm các kí tự từ ~a \rightarrow z~) mô tả từng tên người dùng trong bộ dữ liệu.
• ~m~ dòng tiếp theo, mỗi dòng gồm một chuỗi kí tự (độ dài không vượt quá ~20~ và chỉ gồm các kí tự từ ~a \rightarrow z~) mô tả các tên cần kiểm tra.

Output

• Gồm ~m~ dòng, mỗi dòng tương ứng với ~1~ kí tự ~'0'~ hoặc ~'1'~ tượng trưng không hoặc có tồn tại tên đó trong bộ dữ liệu

Scoring

• Subtask ~1~: Accepted

Sample Input 1

5 5
pitomon
hieuhfgr
tuevd
khanhgay
kimbeo
pito
kimbeo
khanhgay
tuedv
hfgrhieu

Sample Output 1

0
1
1
0
0

Sample Input 2

1 5
pitomondepchaivai
pitomonxautraiqua
kimkhongdepchai
pitodepchaivai
chaichaichaichai
pitomondepchaivai

Sample Output 2

0
0
0
0
1

Giải thích

Đề dễ quá từ chối giải thích

Công chúa nước Gama nổi tiếng rất thông minh, nhà vua cần tìm một người để dạy học cho công chúa. Hôm nay nhà vua mở một cuộc thi tuyển với hi vọng chọn được người thầy như mong đợi. Cuộc thi tuyển gồm ~2~ vòng, vòng thứ nhất gồm ~P~ người đến từ khắp nơi trong vương quốc và các nước láng giềng tham dự, họ đều có học vấn rất uyên bác. Bắt đầu cuộc thi, công chúa phát cho ~P~ người thi tuyển mỗi người một cái túi thơm trong đó có chứa một thẻ bài, trên mỗi thẻ bài có ghi một số tự nhiên ~N~. Khi phát túi thơm đến người cuối cùng công chúa sẽ đếm từ một đến ba, tất cả người dự thi mở túi thơm của mình ra, sử dụng trí thông minh và học vấn uyên bác trả lời câu hỏi mà công chúa yêu cầu:

Với số ~N~ trên thẻ bài của mình, mỗi người dự thi phải tìm các thừa số nguyên tố được phân tích từ tích các số tự nhiên từ ~1~ đến ~N~. Sau đó tính tổng các thừa số và các số mũ tương ứng.

Giả sử với ~N=4~ thì các thừa số được phân tích từ kết quả: ~1×2×3×4=24~ là ~2^3×3^1~ sau đó tổng cộng tất cả các thừa số và số mũ tương ứng ~2+3+3+1 = 9~. Trong thời gian ba phút, người nào trả lời được đúng kết quả theo yêu cầu của công chúa thì được thi tiếp vòng ~2~.

Yêu cầu

Em hãy lập trình giúp công chúa kiểm tra kết quả theo yêu cầu trên.

Input

Từ tệp TUYENCHON.INP chứa một số tự nhiên ~N~.

Output

Ghi vào tệp TUYENCHON.OUT một số tự nhiên duy nhất là kết quả theo yêu cầu.

Sample Input 1

4

Sample Output 1

9

Giải thích

Minh họa kết quả của một người:

• Với ~N=4~, ta có: ~1×2×3×4=24~.
• Phân tích ~24~: ~2^3×3^1~. Kết quả: ~2+3+3+1=9~

Ràng buộc

• ~50\%~ số điểm ứng với ~50\%~ số test có ~3 \leq N \leq 100~
• ~50\%~ số điểm ứng với ~50\%~ số test không có ràng buộc thêm.

Roger đang lập trình một trò chơi khá thú vị để thử thách người chơi là Peter. Trong trò chơi này có một mê cung rộng lớn với ~N~ điểm dừng và ~M~ con đường hai chiều nối giữa các điểm dừng. Mê cung mà Roger tạo ra luôn đảm bảo giữa hai điểm dừng luôn tồn tại một đường đi trực tiếp hoặc gián tiếp nối với chúng.

Để tăng độ thú vị cho trò chơi, trên mỗi con đường trực tiếp nối giữa hai điểm dừng có thể đặt một con quái vật (Boss). Nếu người chơi đi qua những con đường có đặt Boss, nhiệm vụ của họ là chuẩn bị chiến thuật và vũ khí để chiến đấu và chiến thắng Boss.

Tại thời điểm bắt đầu của trò chơi, Roger sẽ chọn điểm dừng xuất phát là ~S~ và điểm dừng kết thúc là ~T~. Sau đó, nhiệm vụ của Peter là sẽ xuất phát từ điểm dừng ~S~, đi qua các con đường để đến được điểm dừng ~T~ và Roger cần phải đặt những con Boss trên những con đường trực tiếp, nằm trên đường đi từ ~S~ đến ~T~, mà Peter chắc chắn phải đi qua. Roger luôn tìm được cách chọn ~S~ và ~T~ sao cho anh ta có thể đặt được nhiều con Boss nhất. Hãy giúp Peter xác định số con Boss mà Roger đã đặt.

Input

Đọc từ tệp MAZE.INP gồm:

• Dòng đầu tiên chứa hai số nguyên ~N~ và ~M \ (2 \leq N \leq 3.10^5)~ là số điểm dừng và số con đường trong mê cung.
• ~M~ dòng tiếp theo, mỗi dòng gồm hai số ~x~ và ~y \ (1 \leq x, y \leq N, x \neq y)~ mô tả đường đi nối giữa hai điểm dừng.
• Bộ dữ liệu được đảm bảo rằng không có hai điểm dừng nào được kết nối bởi hai hoặc nhiều hơn hai con đường và mỗi điểm dừng có thể đi đến tất cả các điểm dừng còn lại.

Output

Ghi ra tệp MAZE.OUT một số nguyên duy nhất là số lượng con Boss mà Roger đã đặt.

Sample Input 1

5 5
1 2
2 3
3 1
4 1
5 2

Sample Output 1

2

Giải thích

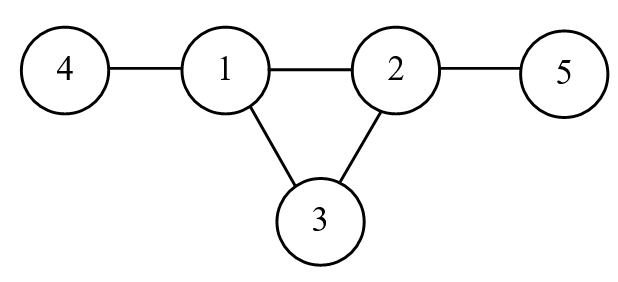
Roger chọn ~S=4~, ~T=5~ thì để đi từ ~S~ đến ~T~ Peter buộc phải đi qua ~2~ đoạn đường là ~(4,1)~ và ~(2,5)~.

Ràng buộc

• Có 20% số test tương ứng với ~M = N - 1~.
• Có 80% số test tương ứng với ~2 \leq N \leq 3.10^5, 1 \leq M \leq 3.10^5~.